SymPy-demo 1: Matrixalgebra og determinanter

Demo af Jakob Lemvig, Christian Mikkelstrup, Hans Henrik Hermansen, Karl Johan Måstrup Kristiansen og Magnus Troen. Revideret 18-10-24 af shsp.

from sympy import *
init_printing()

Matricer og ligningsystemer

Et lineært ligningssystem med én løsning

Vi vil gerne løse det lineære ligningssystem

\[\begin{split}\begin{aligned} -x_2+x_3&=2\\ 2x_1+4x_2-2x_3&=2\\ 3x_1+4x_2+x_3&=9.\\ \end{aligned}\end{split}\]

Dette kan gøres på adskillige måder - lad os gennemgå nogle metoder i de følgende underafsnit.

Metode 0 - Definér alle ligningerne

En mulighed er simpelthen at definere alle ligningerne og bede SymPy om at løse dem.

x1,x2,x3 = symbols('x1:4')
eq1 = Eq(-x2 + x3, 2)
eq2 = Eq(2*x1 + 4*x2 - 2*x3, 2)
eq3 = Eq(3*x1 + 4*x2 + x3, 9)
eq1, eq2, eq3

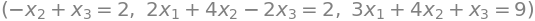
Lineære ligningsystemer kan i SymPy løses med linsolve()-kommandoen:

linsolve((eq1,eq2,eq3), (x1,x2,x3))

Systemet har altså præcis en løsning:

\[\begin{split} \begin{bmatrix} x_1 \\ x_2 \\ x_3\end{bmatrix} = \begin{bmatrix} 4 \\ -1 \\ 1\end{bmatrix}. \end{split}\]

Metode 1 - Konvertér systemet til matrixform

En anden tilgang til at løse et ligningssystem er, når du har systemets koefficientmatrix \(\mathbf A\) og højreside \(\mathbf b\). Da vi allerede har defineret ligningerne ovenfor, kan kommandoen linear_eq_to_matrix() benyttes til at opstille denne matrix og vektor.

A,b = linear_eq_to_matrix([eq1,eq2,eq3],[x1,x2,x3])
A,b

\[\begin{split}\displaystyle \left( \left[\begin{matrix}0 & -1 & 1\\2 & 4 & -2\\3 & 4 & 1\end{matrix}\right], \ \left[\begin{matrix}2\\2\\9\end{matrix}\right]\right)\end{split}\]

Definér matricer

Du vil ofte skulle definere din matrix manuelt. Dette gøres med kommandoen Matrix():

A = Matrix([
    [0,-1,1],
    [2,4,-2],
    [3,4,1]])
A

\[\begin{split}\displaystyle \left[\begin{matrix}0 & -1 & 1\\2 & 4 & -2\\3 & 4 & 1\end{matrix}\right]\end{split}\]

Dit input i denne kommando skal være matricens række som lister adskildt af komma. Bemærk, at der også skal tilføjes en omkransende [...] omkring alle listerne. Pas på ikke fejlagtigt at tro, at dine lister vil blive sat sammen som kolonner i matricen - tjek altid dit output nøje efter.

En alternativ måde at indtaste elementerne i Matrix()-kommandoen på er følgende, hvor du udfylder det angivne antal rækker og kolonner rækkevis fra venstre mod højre:

Matrix(3,2,[1,2,3,4,5,6])

\[\begin{split}\displaystyle \left[\begin{matrix}1 & 2\\3 & 4\\5 & 6\end{matrix}\right]\end{split}\]

Definér vektorer

En vektor defineres ved brug af samme kommando som for en matrix. Her udelades blot den omkransende [...], og kun én liste indtastes. Denne liste vil blive fortolket som en søjle, og du har dermed en søjlevektor:

b = Matrix([2,2,9])
A,b

\[\begin{split}\displaystyle \left( \left[\begin{matrix}0 & -1 & 1\\2 & 4 & -2\\3 & 4 & 1\end{matrix}\right], \ \left[\begin{matrix}2\\2\\9\end{matrix}\right]\right)\end{split}\]

Altså, vi definerer matricer ved at angive en liste af lister, hvor hver indre liste angiver en række, mens vi definerer søjlevektorer ved kun at angive én liste og ikke andet:

• Matrix([[a,b,c],[d,e,f],[g,h,i]]) genererer \(\displaystyle{\begin{bmatrix} a & b & c\\ d & e & f\\ g & h & i \end{bmatrix}}.\)

• Matrix([a,b,c]) genererer \(\displaystyle{\begin{bmatrix} a\\b\\c \end{bmatrix}}.\)

Løs ved brug af matrixformen

Det er en typisk fejl at glemme den omsluttende [...] omkring listerne af rækker, når man definerer en matrix. Python vil da give en fejl, som du kan formatere som følger hvis ønsket:

# Eksempel på forkert defineret matrix
try:
    Matrix([1,2,3], [4,5,6], [7,8,9])
except:
    print("Et ydre sæt [] om rækkerne er nødvendig")

Et ydre sæt [] om rækkerne er nødvendig

Kommandoen linsolve() fra Metode 0 ovenfor kan også tage matricer som input: linsolve((A,b)).

Når en koefficientmatrix \(\mathbf A\) og en højreside \(\mathbf b\) er defineret, finder linsolve() vores løsning:

linsolve((A,b))

Metode 2 - Gauss-elimination og reduceret trappeform

Gauss-Jordan solve

Har man opskrevet koefficientmatricen og systemets højreside, kan SymPy også løse systemet ved Gauss-Jordan-metoden med .gauss_jordan_solve(højreside).

A.gauss_jordan_solve(b)

\[\begin{split}\displaystyle \left( \left[\begin{matrix}4\\-1\\1\end{matrix}\right], \ \left[\begin{matrix}\end{matrix}\right]\right)\end{split}\]

Denne metode er generelt meget overskuelig fra et brugersynspunkt. Men den resulterer i en \(\verb|ValueError|\)-fejlmelding, hvis ligningsystemet ikke har nogen løsninger.

A2 = Matrix(2,2, [1,2,0,0])
b_uden_losning = Matrix([1,2])

try:
    A2.gauss_jordan_solve(b_uden_losning)
except Exception as e:
    print(e)

Linear system has no solution

Reduceret trappeform

Alternativt kan man opskrive totalmatrixen, som man ville gøre det i hånden:

\[ \mathbf{T} = [\mathbf{A} | \mathbf{b}]. \]

T = Matrix.hstack(A,b)
T

\[\begin{split}\displaystyle \left[\begin{matrix}0 & -1 & 1 & 2\\2 & 4 & -2 & 2\\3 & 4 & 1 & 9\end{matrix}\right]\end{split}\]

Herefter kan den reducerede trappeform (reduced row-echelon form, rref) findes med .rref().

T.rref(pivots = False)

\[\begin{split}\displaystyle \left[\begin{matrix}1 & 0 & 0 & 4\\0 & 1 & 0 & -1\\0 & 0 & 1 & 1\end{matrix}\right]\end{split}\]

Igen ser vi, at løsningen er \(x_1 = 4\), \(x_2 =-1\) og \(x_3 =1 \).

pivots = False angiver blot, at vi ikke er interreserede i, hvilke søjler der indeholder pivotelementer. Uden dette argument fås følgende output, hvor der er en smule mere information i outputtet:

T.rref()

\[\begin{split}\displaystyle \left( \left[\begin{matrix}1 & 0 & 0 & 4\\0 & 1 & 0 & -1\\0 & 0 & 1 & 1\end{matrix}\right], \ \left( 0, \ 1, \ 2\right)\right)\end{split}\]

Metode 3 - Simuleret håndregning

SymPy giver også mulighed for at udføre Gauss-Jordan-elimination trin for trin, det vil sige at udføre elementære rækkeoperationer som man ville gøre det manuelt. Dette er brugbart, når du ikke ønsker en fuld reduktion af din matrix eller den endelige løsning med det samme, fordi du skal bruge indsigt i de mellemtrin, der opstår undervejs. At bruge SymPy til at udføre rækkeoperationer på denne måde kalder vi simuleret håndregning.

For at nå frem til den reducerede trappeform, arbejder vi på hver søjle én ad gangen. For at bearbejde den første søjle ombytter vi først række 1 og række 2, derefter ganger vi den nye række 1 med \(1/2\), og til sidst tilføjer vi \(-3\) gange række 1 til række 3. Bemærk SymPy-syntaksen for disse tre typer rækkeoperationer i det følgende:

T1 = T.elementary_row_op('n<->m', 0, 1)
T2 = T1.elementary_row_op('n->kn', 0, S(1)/2)
T3 = T2.elementary_row_op('n->n+km',2,-3,0)
T1,T2,T3

\[\begin{split}\displaystyle \left( \left[\begin{matrix}2 & 4 & -2 & 2\\0 & -1 & 1 & 2\\3 & 4 & 1 & 9\end{matrix}\right], \ \left[\begin{matrix}1 & 2 & -1 & 1\\0 & -1 & 1 & 2\\3 & 4 & 1 & 9\end{matrix}\right], \ \left[\begin{matrix}1 & 2 & -1 & 1\\0 & -1 & 1 & 2\\0 & -2 & 4 & 6\end{matrix}\right]\right)\end{split}\]

Nu bearbejder vi de sidste to søjler som følger:

T4 = T3.elementary_row_op('n->kn',1,-1)
T5 = T4.elementary_row_op('n->n+km',2,2,1)
T6 = T5.elementary_row_op('n->n+km',0,-2,1)
T4,T5,T6

\[\begin{split}\displaystyle \left( \left[\begin{matrix}1 & 2 & -1 & 1\\0 & 1 & -1 & -2\\0 & -2 & 4 & 6\end{matrix}\right], \ \left[\begin{matrix}1 & 2 & -1 & 1\\0 & 1 & -1 & -2\\0 & 0 & 2 & 2\end{matrix}\right], \ \left[\begin{matrix}1 & 0 & 1 & 5\\0 & 1 & -1 & -2\\0 & 0 & 2 & 2\end{matrix}\right]\right)\end{split}\]

T7 = T6.elementary_row_op('n->kn',2,S(1)/2)
T8 = T7.elementary_row_op('n->n+km',0,-1,2)
T9 = T8.elementary_row_op('n->n+km',1,1,2)
T7,T8,T9

\[\begin{split}\displaystyle \left( \left[\begin{matrix}1 & 0 & 1 & 5\\0 & 1 & -1 & -2\\0 & 0 & 1 & 1\end{matrix}\right], \ \left[\begin{matrix}1 & 0 & 0 & 4\\0 & 1 & -1 & -2\\0 & 0 & 1 & 1\end{matrix}\right], \ \left[\begin{matrix}1 & 0 & 0 & 4\\0 & 1 & 0 & -1\\0 & 0 & 1 & 1\end{matrix}\right]\right)\end{split}\]

Af denne reducerede trappeform aflæser vi den samme løsning som fra de andre metoder ovenfor.

Denne metode er langt mere krævende men kan være nødvendig, når man løser systemer, der indeholder variable eller ubekendte koefficienter, da SymPy ikke fanger “undtagelser” og “særtilfælde” undervejs i en matrixreduktion. Hvis din matrix fx indeholder en ubekendt, og du undervejs i reduktionen ønsker at udføre en rækkeoperation, der dividerer med et udtryk med ubekendte i, så vil visse værdier af den ubekendte måske føre til division med nul. Disse værdier - som skal behandles som særtilfælde efterfølgende - bliver ignoreret af SymPy.

Et lineært ligningssystem med flere løsninger

Vi ønsker at løse det inhomogene ligningssystem, hvis koefficientmatrix er givet ved

A = Matrix([[1,3,2,4,5],[2,6,4,3,5],[3,8,6,7,6],[4,14,8,10,22]])
A

\[\begin{split}\displaystyle \left[\begin{matrix}1 & 3 & 2 & 4 & 5\\2 & 6 & 4 & 3 & 5\\3 & 8 & 6 & 7 & 6\\4 & 14 & 8 & 10 & 22\end{matrix}\right]\end{split}\]

og hvis højreside er givet ved

b = Matrix([9,3,5,32])
b

\[\begin{split}\displaystyle \left[\begin{matrix}9\\3\\5\\32\end{matrix}\right]\end{split}\]

Metode 1 - Løs direkte i SymPy

Vi har nu set flere forskellige metoder til løsning af et ligningssystem, metoder som selvfølgelig også kan anvendes på inhomogene systemer. Lad os prøve at benytte nogle af dem:

A.gauss_jordan_solve(b)

\[\begin{split}\displaystyle \left( \left[\begin{matrix}- 2 \tau_{0} + 11 \tau_{1} - 24\\7 - 4 \tau_{1}\\\tau_{0}\\3 - \tau_{1}\\\tau_{1}\end{matrix}\right], \ \left[\begin{matrix}\tau_{0}\\\tau_{1}\end{matrix}\right]\right)\end{split}\]

linsolve((A,b))

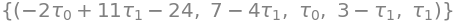
Løsningen indeholder frie parametre (der er uendeligt mange løsninger). SymPy anvender symbolerne \(\tau_0\) og \(\tau_1\) som de frie parametre. De opfylder generelt \(\tau_0, \tau_1 \in \mathbb{F}\).

Ovenstående SymPy-outputs er ikke letlæselige, og vi vil foretrække at præsentere vores løsninger fx på standard parameterform. Derfor vil vi typisk altid opskrive SymPy-outputtet med Latex for en pæn præsentation:

\[\begin{split}\mathbf x= \begin{bmatrix}-24\\7\\0\\3\\0\end{bmatrix} +\tau_0\begin{bmatrix}-2\\0\\1\\0\\0\end{bmatrix}+\tau_1\begin{bmatrix}11\\-4\\0\\-1\\1\end{bmatrix}\quad , \tau_0,\tau_1\in\mathbb F.\end{split}\]

Bemærk, at Python anvender nul-indeksering, så en liste af frie parametre som her vil blive nummereret startende fra \(0\).

Metode 2 - Løs vha. rref()

Vi opskriver først totalmatricen ved:

T = A.row_join(b)
T

\[\begin{split}\displaystyle \left[\begin{matrix}1 & 3 & 2 & 4 & 5 & 9\\2 & 6 & 4 & 3 & 5 & 3\\3 & 8 & 6 & 7 & 6 & 5\\4 & 14 & 8 & 10 & 22 & 32\end{matrix}\right]\end{split}\]

Dernæst finder vi den reducerede trappeform:

T.rref()

\[\begin{split}\displaystyle \left( \left[\begin{matrix}1 & 0 & 2 & 0 & -11 & -24\\0 & 1 & 0 & 0 & 4 & 7\\0 & 0 & 0 & 1 & 1 & 3\\0 & 0 & 0 & 0 & 0 & 0\end{matrix}\right], \ \left( 0, \ 1, \ 3\right)\right)\end{split}\]

Vi kan nemt aflæse løsningen til at være:

\[\begin{split} \begin{bmatrix}x_1\\x_2\\x_3\\x_4\\x_5 \end{bmatrix}= \begin{bmatrix}-24\\7\\0\\3\\0 \end{bmatrix}+ \tau_0\begin{bmatrix}-2\\0\\1\\0\\0 \end{bmatrix}+\tau_1\begin{bmatrix}11\\-4\\0\\-1\\1\end{bmatrix} \quad , \tau_0,\tau_1\in\mathbb F. \end{split}\]

Vi udelod argumentet pivots=False fra kommandoen denne gang for klart at kunne se, hvilke søjler der indeholder pivotter. Der er ingen pivotter i søjle 3 og 5, hvorfor variablerne \(x_3\) og \(x_5\) bliver vores frie parametre \(\tau_0\) og \(\tau_1\) i dette eksempel.

Check

Lad os tjekke efter, at antallet af frie parametre er korrekt. Vi fandt frem til to i det ovenstående.

Antallet af ubekendte er \(n=5\), så antallet af frie parametre skal gerne være lig med \(n-\rho(\mathbf A)\), hvor \(\rho\) er matricens rang.

A.rank()

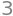
5-A.rank()

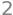
Som forventet.

Matrixalgebra

Grundlæggende matrixalgebra og matrixaritmetik

Vi vil benytte følgende matricer til eksemplerne i dette afsnit:

A = Matrix([[2,1],[3,0],[7,11]])
B = Matrix([[1,1],[9,3],[-7,-1]])
C = Matrix([[2,1,3],[-6,5,8]])
A,B,C

\[\begin{split}\displaystyle \left( \left[\begin{matrix}2 & 1\\3 & 0\\7 & 11\end{matrix}\right], \ \left[\begin{matrix}1 & 1\\9 & 3\\-7 & -1\end{matrix}\right], \ \left[\begin{matrix}2 & 1 & 3\\-6 & 5 & 8\end{matrix}\right]\right)\end{split}\]

Vi kan gange matricen \(\mathbf A\) med en konstant ved:

k = symbols('k')
k*A

\[\begin{split}\displaystyle \left[\begin{matrix}2 k & k\\3 k & 0\\7 k & 11 k\end{matrix}\right]\end{split}\]

Da \(\mathbf A\) og \(\mathbf B\) er af samme type, \(\mathbb{R}^{3\times 2}\), er matrixsummen \(\mathbf A+\mathbf B\) defineret.

A+B

\[\begin{split}\displaystyle \left[\begin{matrix}3 & 2\\12 & 3\\0 & 10\end{matrix}\right]\end{split}\]

Vi kan også udregne linearkombinationer af matricer, for eksempel \(3A-5B\):

3*A-5*B

\[\begin{split}\displaystyle \left[\begin{matrix}1 & -2\\-36 & -15\\56 & 38\end{matrix}\right]\end{split}\]

Da antallet af søjler i \(\mathbf A\) passer med antallet af rækker i \(\mathbf C\), kan vi bestemme matrixproduktet \(\mathbf A \cdot \mathbf C\).

A*C

\[\begin{split}\displaystyle \left[\begin{matrix}-2 & 7 & 14\\6 & 3 & 9\\-52 & 62 & 109\end{matrix}\right]\end{split}\]

Bemærk, at matrixprodukter ikke nødvendigvis kommuterer, så generelt er \(\mathbf A\mathbf C \neq \mathbf C\mathbf A\), hvilket det følgende viser tydeligt:

display(A*C, C*A)

\[\begin{split}\displaystyle \left[\begin{matrix}-2 & 7 & 14\\6 & 3 & 9\\-52 & 62 & 109\end{matrix}\right]\end{split}\]

\[\begin{split}\displaystyle \left[\begin{matrix}28 & 35\\59 & 82\end{matrix}\right]\end{split}\]

Den transponerede matrix kan findes med adskillige forskellige kommandoer:

A.T, A.transpose(), transpose(A)

\[\begin{split}\displaystyle \left( \left[\begin{matrix}2 & 3 & 7\\1 & 0 & 11\end{matrix}\right], \ \left[\begin{matrix}2 & 3 & 7\\1 & 0 & 11\end{matrix}\right], \ \left[\begin{matrix}2 & 3 & 7\\1 & 0 & 11\end{matrix}\right]\right)\end{split}\]

Rangen af en marix kan findes ved:

A.rank()

Hvis en matrix er invertibel, kan dens inverse matrix bestemmes med .inv():

M = Matrix([[2,0,1],[1,2,0],[-2,1,4]])

M*M.inv()

\[\begin{split}\displaystyle \left[\begin{matrix}1 & 0 & 0\\0 & 1 & 0\\0 & 0 & 1\end{matrix}\right]\end{split}\]

Indexering i matrixer

Elementer i en matrix kan tilgås ved, at matricen opfattes som et 2D array. Kommandoen M[n,m], hvor M er en matrix, vil give os elementet placeret i række \(n\) og kolonne \(m\). Her er det særligt vigtigt at huske, at Python bruger nulindeksering.

Lad os se på matricen:

M = Matrix([[2,0,1],[1,2,0],[-2,1,4]])
M

\[\begin{split}\displaystyle \left[\begin{matrix}2 & 0 & 1\\1 & 2 & 0\\-2 & 1 & 4\end{matrix}\right]\end{split}\]

Elementet i række 3 og i søjle 3 kan altså fås ved:

M[2,2]

Skal vi have fat i en hel søjle benyttes M.col()-kommandoen. Det følgende vil give dig søjle 2:

M.col(1)

\[\begin{split}\displaystyle \left[\begin{matrix}0\\2\\1\end{matrix}\right]\end{split}\]

For rækker har vi den tilsvarende M.row().

M.row(0)

\[\displaystyle \left[\begin{matrix}2 & 0 & 1\end{matrix}\right]\]

Vi kan være endnu mere sofistikerede i vores håndtering af indholdet i en matrix. Hvis vi ønsker at fjerne den første række og den sidste kolonne, så fortæller vi blot SymPy, at vi kun vil have de sidste to rækker og de første to kolonner. Dette gør vi ved at bruge slices som følger:

M[1:, :2]

\[\begin{split}\displaystyle \left[\begin{matrix}1 & 2\\-2 & 1\end{matrix}\right]\end{split}\]

Læs mere om slicing i Python ved en internetsøgning.

SymPy kan anvendes til at udtrække en snitmatrix. Vi ville matematisk anvende notation \(\mathbf A(i; j)\) for en matrix, der er identisk med den gamle matrix men uden række \(i\) og søjle \(j\) (se lærebogen for mere). Kommandoen til dette i SymPy er M.minorMatrix(i,j).

M.minorMatrix(0,-1)

\[\begin{split}\displaystyle \left[\begin{matrix}1 & 2\\-2 & 1\end{matrix}\right]\end{split}\]

Determinanter

Vi betragter følgende matrix:

\[\begin{split} \mathbf A = \begin{bmatrix} 0 & 2 & 3 & 4 \\ 2 & 0 & 4 & 3 \\ 3 & 4 & 0 & 2 \\ 4 & 3 & 2 & 0\end{bmatrix}. \end{split}\]

For at finde determinanten her, benytter vi SymPys indbyggede kommando:

A = Matrix([[0,2,3,4],[2,0,4,3],[3,4,0,2],[4,3,2,0]])
A.det()

eller tilsvarende:

det(A)

Determinanten af en snitmatrix \(\det(\mathbf M(i;j))\) kan selvfølgelig beregnes ved først at bestemme snitmatricen og derefter at finde dens determinant, så det(M.minorMatrix(i,j)). Men der findes også en direkte kommando, der skrives direkte på den oprindelige matrix: M.minor(i,j).

det(M.minorMatrix(0,-1)), M.minor(0,-1)

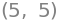
Anvendelser af determinanter

Existens af invers matrix

Betragt matrixen

\[\begin{split} \mathbf A = \left[\begin{matrix}1 & 2 & 3\\2 & 4 & 1\\3 & a & 7\end{matrix}\right]. \end{split}\]

Vi ønsker at bestemme \(a \in \mathbb{R}\), således at \(\mathbf A\) er invertibel. Ifølge lærebogen er \(\mathbf A\) invertibel, hvis og kun hvis \(\operatorname{det}(\mathbf A) \neq 0\). Derfor vil vi løse

\[ \operatorname{det}(\mathbf A) = 0 \]

for \(a\). Dette vil give os alle \(a\)-værdier, for hvilke \(\mathbf A\) ikke er invertibel. Vi udfører dette som følger:

a = symbols('a', real = True)
A = Matrix([[1,2,3],[2,4,1],[3,a,7]])
A

\[\begin{split}\displaystyle \left[\begin{matrix}1 & 2 & 3\\2 & 4 & 1\\3 & a & 7\end{matrix}\right]\end{split}\]

solveset(Eq(det(A), 0), a, S.Reals)

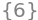
Altså er \(\mathbf A\) invertibel for \(a \in \mathbb{R}\setminus\{6\}\).

Lineær (u)afhængighed

Betragt følgende fire vektorer i \(\mathbb{C}^4\):

\[\begin{split} \mathbf v_1 = \left[\begin{matrix}1 + i\\3\\0\\7 i\end{matrix}\right], \ \mathbf v_2 = \left[\begin{matrix}2\\4 - i\\2 i\\8 - i\end{matrix}\right], \ \mathbf v_3 = \left[\begin{matrix}3 + i\\7 - i\\2 i\\8 + 6 i\end{matrix}\right], \ \mathbf v_4 = \left[\begin{matrix}3\\-1 - i\\7 i\\0\end{matrix}\right]. \end{split}\]

v1 = Matrix([1+I, 3, 0 , 7*I])
v2 = Matrix([2, 4-I, 2*I, 8-I])
v3 = Matrix([3+I, 7-I, 2*I, 8+6*I])
v4 = Matrix([3,-1-I, 7*I, 0])

Det ønskes at undersøge, hvorvidt \(\mathbf v_1,\mathbf v_2,\mathbf v_3,\mathbf v_4\) er lineært uafhængige. Først opstiller vi matricen

\[ \mathbf A = [\mathbf v_1,\mathbf v_2,\mathbf v_3,\mathbf v_4]. \]

A = Matrix.hstack(v1,v2,v3,v4)
A

\[\begin{split}\displaystyle \left[\begin{matrix}1 + i & 2 & 3 + i & 3\\3 & 4 - i & 7 - i & -1 - i\\0 & 2 i & 2 i & 7 i\\7 i & 8 - i & 8 + 6 i & 0\end{matrix}\right]\end{split}\]

Vi udregner nu determinanten af denne matrix:

det(A)

Da \(\det(\mathbf A) = 0\), kan vi konkludere, at vektorerne \(\mathbf v_1,\mathbf v_2,\mathbf v_3,\mathbf v_4\) er lineært afhængige (se den relevante sætning i kursuslærebogen).

Lad os nu kun fokusere på \(\mathbf v_1,\mathbf v_2,\mathbf v_4\). Er denne mængde af blot tre af vektorerne lineært uafhængig? Da \(\mathbf B = [\mathbf v_1,\mathbf v_2,\mathbf v_4] \in \mathbb{C}^{4 \times 3}\) ikke er en kvadratisk matrix, kan vi ikke udregne en determinant, og derfor kan vi ikke benytte metoden ovenfor. I stedet vil vi se på deres linearkombination og undersøge, om der findes koefficienter, der ikke er nul, således at denne linearkombination er lig med nul (se kursuslærebogen for mere).

Lad \(c_1,c_2,c_3 \in \mathbb{C}\) være vilkårlige skalarer, og antag

\[ c_1 \mathbf v_1 + c_2 \mathbf v_2 + c_3 \mathbf v_4 = 0. \]

Dette svarer til et ligningssystem, hvis koefficientmatrix udgøres af de tre vektorer som søjler. Vi løser dette system:

cs = symbols('c:3')
B = Matrix.hstack(v1,v2,v4)
linsolve((B,zeros(4,1)), cs)

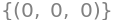
Den eneste løsning er \(c_1 = c_2 = c_3 = 0\). Derfor er \(\mathbf v_1,\mathbf v_2,\mathbf v_4\) lineært uafhængige.

Tips og tricks til matrixkonstruktion

Nogle foretrækker at opskrive matricer i SymPy som følger:

Matrix(3,3,[1,2,3,4,5,6,7,8,9])

\[\begin{split}\displaystyle \left[\begin{matrix}1 & 2 & 3\\4 & 5 & 6\\7 & 8 & 9\end{matrix}\right]\end{split}\]

Her angiver (3,3) dimensionen, og rækkerne i matricen indtastes nu som en enkelt liste, [1,2,3,...], fremfor at indtaste en liste per række.

Enhedsmatricer laves nemt i SymPy ved eye(dimension):

eye(3), eye(3,2)

\[\begin{split}\displaystyle \left( \left[\begin{matrix}1 & 0 & 0\\0 & 1 & 0\\0 & 0 & 1\end{matrix}\right], \ \left[\begin{matrix}1 & 0\\0 & 1\\0 & 0\end{matrix}\right]\right)\end{split}\]

Diagonalmatricer kan defineres ved Matrix.diag(elementer):

Matrix.diag([1,2,3,4,5])

\[\begin{split}\displaystyle \left[\begin{matrix}1 & 0 & 0 & 0 & 0\\0 & 2 & 0 & 0 & 0\\0 & 0 & 3 & 0 & 0\\0 & 0 & 0 & 4 & 0\\0 & 0 & 0 & 0 & 5\end{matrix}\right]\end{split}\]

Fulde 0-matricer eller 1-matricer kan opnås med zeros(m, n) og ones(m, n):

zeros(2), ones(3,2)

\[\begin{split}\displaystyle \left( \left[\begin{matrix}0 & 0\\0 & 0\end{matrix}\right], \ \left[\begin{matrix}1 & 1\\1 & 1\\1 & 1\end{matrix}\right]\right)\end{split}\]

\(\verb|ones(m,n)|\) kan anvendes til at opstille en matrix, hvori alle elementer er ens:

k = 7
k * ones(3,2)

\[\begin{split}\displaystyle \left[\begin{matrix}7 & 7\\7 & 7\\7 & 7\end{matrix}\right]\end{split}\]

Mere avancerede matrixkonstruktioner kan gøres med Matrix(m, n, lambda i,j: udtryk), en kommando der afsluttes med argumentet udtryk, som angiver, hvad der skal ske med hvert element. For eksempel:

Matrix(3,2, lambda i,j: 3*i + j)

\[\begin{split}\displaystyle \left[\begin{matrix}0 & 1\\3 & 4\\6 & 7\end{matrix}\right]\end{split}\]

Vi kan fx opstille enhedsmatricen således:

Matrix(3,3, lambda i,j: 1 if i == j else 0)

\[\begin{split}\displaystyle \left[\begin{matrix}1 & 0 & 0\\0 & 1 & 0\\0 & 0 & 1\end{matrix}\right]\end{split}\]