SymPy Demo 6: Differentialligninger og systemer heraf

Demo af Karl Johan Måstrup Kristiansen og Magnus Troen. Revideret 29-10-24 af shsp.

from sympy import *
init_printing()

1.-ordens lineære differentialligninger

Jævnfør en sætning i kursuslærebogen kan en 1.-ordens lineær differentialligning på formen

\[ f'(t) = p(t)f(t) + q(t) \]

løses ved brug af formlen

\[f(t) = \mathrm e^{P(t)}\int \mathrm e^{-P(t)} q(t)\ \mathrm dt, \]

hvor \(P(t)\) er en stamfunktion til \(p(t)\).

Lad os som et eksempel se på følgende inhomogene differentialligning, hvor \(t\in\mathbb{R}\):

\[ f'(t) + 4\cdot f(t) = \mathrm e^{3t}. \]

Vi ønsker at finde den fuldstændige løsning til denne ligning samt en partikulær løsning, der opfylder følgende begyndelsesværdibetingelse:

\[f(1) = 5.\]

Løs ved (simuleret) håndregning

Den fuldstændige løsning

For at kunne anvende ovenstående formel, skal differentialligningen først omskrives til den nødvendige form:

\[ f'(t) = -4\cdot f(t) + \mathrm e^{3t}. \]

Vi definerer komponenterne \(p(t) = -4\) og \(q(t)=\mathrm e^{3t}\) i SymPy:

t = symbols('t', real = True)

# Definér p(t) og q(t)
pt = -4
qt = exp(3*t)

Vi kan nu opstille integranden (indholdet i integralet i formlen, altså \(\mathrm e^{-P(t)} q(t)\)). Til dette skal vi bruge en \(P(t)\), dvs. en stamfunktion til \(p(t)\), hvilket kan findes ved at integrere \(p(t)\). SymPy har den nemme kommando integrate() til dette formål:

# Find en stamfunktion P(t)
Pt = integrate(pt,t)

# Konstruér integranden
integrand = simplify(exp(-Pt)*qt)
integrand

Bemærk, at SymPy ikke tilføjer en konstant til resultatet efter integration. integrate()-kommandoen finder en enkelt stamfunktion og altså ikke det fulde ubestemte integral. For udregning af integralet i formlen, som vi er i gang med, er denne konstant vigtig, så vi er nødt til manuelt at tilføje en \(c_1 \in \mathbb{F}\) selv:

c1 = symbols('c1')

# Bestem f(t) ved brug af formlen
f_t = exp(Pt)*(integrate(integrand,t) + c1)
f_t

Dette er den fuldstændige løsning.

Vi kunne selvfølgelig forsøge at udføre alt det ovenstående i én kodelinje, altså med noget i stil med følgende:

# Fjern udkommenteringen af følgende linje for at se, om SymPy kan køre det:

# exp(integrate(pt,t))*(integrate(exp(-integrate(pt,t))*qt,t) + c1)

Dette virker muligvis denne gang i dette relativt simple eksempel, men SymPy kan ofte løbe ind i problemer med integrationer, når integranden bliver kompliceret. Sker det, så anbefaler vi, at du opdeler udregningen, som vi har gjort i ovenstående, og finder komponenterne på forhånd, samt at du finder integranden og simplificerer den mest muligt, før integrationen udføres på den.

En partikulær løsning via begyndelsesværdibetingelse

Den fuldstændige løsning \(f(t)\), som vi fandt, består af uendeligt mange løsninger. Dette skyldes konstanten \(c_1\), som kan tage enhver værdi. Kun én partikulær løsning iblandt dem opfylder den givne begyndelsesværdibetingelse \(f(1) = 5.\)

Vi kan finde denne partikulære løsning ved at løse for den værdi af konstanten \(c_1\), der får \(f(t)\) til at opfylde betingelsen:

# Begyndelsesbetingelsen
eq = Eq(f_t.subs(t,1), 5)

# Løs for c_1
c1_sp = solveset(eq, c1).args[0]
c1_sp

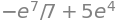
Vi indsætter denne værdi af konstanten i den fuldstændige løsning for at finde vores ønskede partikulære løsning:

f_p = simplify(f_t.subs(c1, c1_sp))
f_p

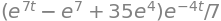
Lad os tjekke efter, at \(f_{p}(t)\) opfylder differentialligningen, som vi startede med, samt at den opfylder begyndelsesværdibetingelsen:

simplify(diff(f_p,t) + 4*f_p) == qt

True

f_p.subs(t,1) == 5

True

Løs direkte med SymPy-kommandoer

Symbolske funktioner

Som du allerede ved alt for godt, kan vi ikke benytte en ubekendt variabel eller konstant i Python, før den er defineret som et symbol ved brug af symbols('variabelnavn'). På tilsvarende vis kan vi ej heller arbejde med en ubekendt funktion, før den er defineret som en symbolsk funktion (symbolic function). Dette kan gøres med kommandoen Function('funktionsnavn'):

t = symbols('t')
f = Function('f')

f(t) , diff(f(t),t) , f(t)+t**3+4

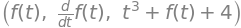
Hvis flere end én funktion skal bruges, kan vi igen benytte os af symbols()-kommandoen, men nu med det ekstra argument cls=Function, der angiver, at vi har med symbolske funktioner at gøre:

f,g,h = symbols('f g h', cls=Function)
f1, f2, f3, f4 = symbols('f1:5', cls=Function)

display([f(t),g(t),h(t)])
display([f1(t), f2(t), f3(t), f4(t)])

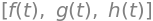
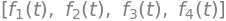
Den fuldstændige løsning via dsolve

Med funktionsnavnet defineret symbolsk kan vi definere og få vist differentialligninger i deres fulde form, før vi løser dem:

ode1 = Eq(diff(f(t),t) + 4*f(t), exp(3*t))
ode1

SymPy kan løse differentialligningen direkte med kommandoen dsolve():

sol = dsolve(ode1)
sol

Bemærk, hvordan outputtet fra dsolve() inkluderer selve funktionsnavnet og har formatet: f(t)=udtryk. For at få fat på dette udtryk, så man kan arbejde videre på det, skal kun højresiden hentes ud:

sol.rhs

En partikulær løsning via dsolve() med begyndelsesværdibetingelser

For at bestemme en partikulær løsning, der opfylder den givne begyndelsesværdibetingelse \(f(1)=5\), tilføjer vi simpelthen betingelsen i et argument til dsolve():

dsolve(ode1, ics={f(1): 5})

Som et alternativ har dtumathtools en wrapper til differentialligningen, der returnerer en dictionary i stedet:

from dtumathtools import *

dtutools.dsolve([ode1], ics = {f(1):5})

Dette er smart senere hen, da det virker med .subs(), så løsningerne nemmere kan bruges i andre dele af dokumentet.

Homogene systemer af lineære 1.-ordens differentialligninger

I kursuslærebogen vil du kunne finde løsningsformler og metoder til de forskellige tilfælde af homogene differentialligningssystemer af orden 1. Vi vil benytte os af en af disse løsningsformler i følgende eksempel.

Som et eksempel får vi for \(t\in\mathbb{R}\) givet følgende system:

\[\begin{split} \begin{cases} f_1'(t) = 2f_1(t) - \frac{1}{2}f_2(t)\\ f_2'(t) = \frac{1}{3}f_1(t) + f_2(t). \end{cases} \end{split}\]

Vi ser straks, at systemet er homogent (da der ikke er nogen forcing functions involveret). Vi vil gerne finde den fuldstændige løsning til systemet samt den partikulære løsning, der opfylder begyndelsesværdibetingelserne \(f_1(0) = 1\) og \(f_2(0) = 0\).

Løs ved (simuleret) håndregning

Den fuldstændige løsning

Systemet kan skrives på matrixform som:

\[\begin{split} \begin{bmatrix} f_1'(t)\\ f_2'(t) \end{bmatrix} = \begin{bmatrix} 2 & -\frac{1}{2}\\ \frac{1}{3} & 1 \end{bmatrix} \begin{bmatrix} f_1(t)\\ f_2(t) \end{bmatrix}. \end{split}\]

Jævnfør et theorem i lærebogen afhænger løsningsstrukturen af egenværdierne til systemets matrix. Så lad os definere denne matrix som \(\mathbf A\):

A = Matrix([[2,-S(1)/2],[S(1)/3, 1]])
A

\[\begin{split}\displaystyle \left[\begin{matrix}2 & - \frac{1}{2}\\\frac{1}{3} & 1\end{matrix}\right]\end{split}\]

og udregne dens egenværdier:

A.eigenvals()

Egenværdierne er reelle men ikke ens, så vi benytter os af en løsningsformel fra lærebogen, der har følgende struktur:

\[ \boldsymbol f(t) = c_1 \mathbf{v}_1 \mathrm e^{\lambda_1 t} + c_2 \mathbf{v}_2 \mathrm e^{\lambda_2 t}, \]

hvor \((\mathbf{v}_i, \lambda_i)\) for \(i = 1,2\) er par af egenvektorer og egenværdier tilhørende systemets matrix, og \(c_1,c_2\in \mathbb{F}\) er konstanter. Husk på, at løsningen - her skrevet som \(\boldsymbol f(t)\) - indeholder to funktioner, \(\boldsymbol f(t)=(f_1(t),f_2(t))\).

Vi har nu også brug for egenvektorer, så vi benytter kommandoen:

ev = A.eigenvects()
ev

\[\begin{split}\displaystyle \left[ \left( \frac{3}{2} - \frac{\sqrt{3}}{6}, \ 1, \ \left[ \left[\begin{matrix}\frac{3}{2} - \frac{\sqrt{3}}{2}\\1\end{matrix}\right]\right]\right), \ \left( \frac{\sqrt{3}}{6} + \frac{3}{2}, \ 1, \ \left[ \left[\begin{matrix}\frac{\sqrt{3}}{2} + \frac{3}{2}\\1\end{matrix}\right]\right]\right)\right]\end{split}\]

Dette gav os alle nødvendige komponenter lige til at indsætte i løsningsstrukturen:

t = symbols('t', real = True)
c1,c2 = symbols('c1,c2')
sol_hom = c1* ev[0][2][0]*exp(ev[0][0]*t) + c2*ev[1][2][0]*exp(ev[1][0]*t)
sol_hom

\[\begin{split}\displaystyle \left[\begin{matrix}c_{1} \left(\frac{3}{2} - \frac{\sqrt{3}}{2}\right) e^{t \left(\frac{3}{2} - \frac{\sqrt{3}}{6}\right)} + c_{2} \left(\frac{\sqrt{3}}{2} + \frac{3}{2}\right) e^{t \left(\frac{\sqrt{3}}{6} + \frac{3}{2}\right)}\\c_{1} e^{t \left(\frac{3}{2} - \frac{\sqrt{3}}{6}\right)} + c_{2} e^{t \left(\frac{\sqrt{3}}{6} + \frac{3}{2}\right)}\end{matrix}\right]\end{split}\]

Dette gav os den fuldstændige løsning til det givne homogene system. Bemærk, hvordan denne løsning er angivet på vektorform, da løsningen udgøres af to funktioner. Den øverste (den første koordinatfunktion i vektoren) er \(f_1(t)\), og den nederste er \(f_2(t)\).

Vi kan tjekke, om dette er korrekt, ved at bekræfte, at

\[\begin{split} \begin{bmatrix}f_1'(t)\\f_2'(t)\end{bmatrix} - \mathbf{A}\begin{bmatrix} f_1(t)\\f_2(t)\end{bmatrix} = \mathbf{0}. \end{split}\]

simplify(diff(sol_hom, t) - A*sol_hom)

\[\begin{split}\displaystyle \left[\begin{matrix}0\\0\end{matrix}\right]\end{split}\]

En partikulær løsning fra begyndelsesværdibetingelse

Som tidligere indeholder den fuldstændige løsning uendeligt mange løsninger. Vi vil nu finde en partikulær løsning iblandt dem, der opfylder de givne begyndelsesbetingelser \(f_1(0)=1\) og \(f_2(0)=0\). Med andre ord, vi vil bestemme værdier af \(c_1\) og \(c_2\), således at \(\begin{bmatrix}f_1(0)\\f_2(0)\end{bmatrix}=\begin{bmatrix}1\\0\end{bmatrix}.\)

En partikulær løsning til dette system vil bestå af to funktioner, \(f_1(t)\) og \(f_2(t)\), og hver af de givne betingelser tilhører blot én af disse funktioner. Så vi er nødt til manuelt at plukke hver funktion ud af den fuldstændige løsning for at kunne indsætte betingelserne:

sol_sp = zeros(2,1)
sol_sp[0] = sol_hom[0].subs(t,0)
sol_sp[1] = sol_hom[1].subs(t,0)
b = Matrix([1,0])
sol_sp,b

\[\begin{split}\displaystyle \left( \left[\begin{matrix}c_{1} \left(\frac{3}{2} - \frac{\sqrt{3}}{2}\right) + c_{2} \left(\frac{\sqrt{3}}{2} + \frac{3}{2}\right)\\c_{1} + c_{2}\end{matrix}\right], \ \left[\begin{matrix}1\\0\end{matrix}\right]\right)\end{split}\]

Her har vi indsat værdien af \(t\) (som er \(t=0\) for dem begge) ind i hver funktion, hvorefter vi har defineret højresiden som en vektor \(\mathbf b\).

Vi vil nu løse disse to ligninger samtidig. Når man løser flere ligninger med solve() samtidig, skal alle ligninger angives som homogene ligninger uden den sædvanlige Eq(). Du skal ikke skrive:

\[ \verb|solve(Eq(sol_sp,b))| \]

men i stedet:

\[ \verb|solve([sol_sp - b])| \]

cs = solve([sol_sp - b])
cs

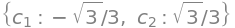
En anden metode er at skrive ligningerne på matrixform for derefter at anvende linssolve() på dem:

B,b = linear_eq_to_matrix(sol_sp - b, [c1,c2])
display((B, b))
linsolve((B, b))

\[\begin{split}\displaystyle \left( \left[\begin{matrix}\frac{3}{2} - \frac{\sqrt{3}}{2} & \frac{\sqrt{3}}{2} + \frac{3}{2}\\1 & 1\end{matrix}\right], \ \left[\begin{matrix}1\\0\end{matrix}\right]\right)\end{split}\]

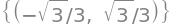
Uanset dit valg af metode, så har du nu fundet frem til følgende partikulære løsning, der opfylder de givne begyndelsesværdibetingelser (husk igen på, at første udtryk i vektoren repræsenterer \(f_{1p}(t)\) og andet udtryk \(f_{2p}(t)\)):

sol_hom.subs(cs)

\[\begin{split}\displaystyle \left[\begin{matrix}- \frac{\sqrt{3} \left(\frac{3}{2} - \frac{\sqrt{3}}{2}\right) e^{t \left(\frac{3}{2} - \frac{\sqrt{3}}{6}\right)}}{3} + \frac{\sqrt{3} \left(\frac{\sqrt{3}}{2} + \frac{3}{2}\right) e^{t \left(\frac{\sqrt{3}}{6} + \frac{3}{2}\right)}}{3}\\- \frac{\sqrt{3} e^{t \left(\frac{3}{2} - \frac{\sqrt{3}}{6}\right)}}{3} + \frac{\sqrt{3} e^{t \left(\frac{\sqrt{3}}{6} + \frac{3}{2}\right)}}{3}\end{matrix}\right]\end{split}\]

Løs direkte med SymPys dsolve()

Igen definerer vi vores differentialligninger ved brug af symbolic functions. Lad os først definere funktionerne:

f1 = Function('f1')
f2 = Function('f2')

f = Matrix([f1(t),f2(t)])
f

\[\begin{split}\displaystyle \left[\begin{matrix}f_{1}{\left(t \right)}\\f_{2}{\left(t \right)}\end{matrix}\right]\end{split}\]

Når du nu skal definere systemet, skal du igen ikke benytte Eq()! Opskriv i stedet systemet med alt på den ene side af et lighedstegn:

\[\begin{split} \begin{bmatrix} f_1'(t) \\ f_2'(t)\end{bmatrix} = \mathbf{A} \begin{bmatrix} f_1(t)\\ f_2(t) \end{bmatrix} \quad\Leftrightarrow\quad \begin{bmatrix} f_1'(t) \\ f_2'(t)\end{bmatrix} - \mathbf{A} \begin{bmatrix} f_1(t)\\ f_2(t)\end{bmatrix} =\mathbf 0 \quad\Leftrightarrow\quad \boldsymbol f'(t)-\mathbf A\cdot \boldsymbol f(t)=\mathbf 0, \end{split}\]

hvor \(\boldsymbol f'(t)\) blot symboliserer, at alle funktionerne inde i \(\boldsymbol f\) skal differentieres. Definér dernæst \(\boldsymbol f'(t)-\mathbf A\cdot \boldsymbol f(t)\) i SymPy. Systemets matrix \(\mathbf A\) har vi allerede defineret ovenfor som A, så alt, vi skal gøre nu, er:

df = diff(f,t)

ode_sys = df - A * f
ode_sys

\[\begin{split}\displaystyle \left[\begin{matrix}- 2 f_{1}{\left(t \right)} + \frac{f_{2}{\left(t \right)}}{2} + \frac{d}{d t} f_{1}{\left(t \right)}\\- \frac{f_{1}{\left(t \right)}}{3} - f_{2}{\left(t \right)} + \frac{d}{d t} f_{2}{\left(t \right)}\end{matrix}\right]\end{split}\]

Vi er nu klar til at løse systemet med en enkelt SymPy-kommando. Som før har vi to muligheder: SymPys version og dtumathtools-versionen. Den eneste forskel er typen af output, da dsolve() returnerer en liste af ligninger, mens dtutools.dsolve() returnerer en dictionary med hver funktion parret med sin tilhørende højreside:

dtutools.dsolve(ode_sys, ics = {f1(0):1, f2(0):0})

dsolve(ode_sys, ics = {f1(0):1, f2(0):0})

Vi har nu den partikulære løsning, der opfylder de givne begyndelsesværdibetingelser. Hvis du skal have den fuldstændige løsning i stedet, så fjern blot ics-argumentet.